(1)
Protein structure / RNA aptamer structure

 Protein is a
sequence of amino acids
of length typically less than
1,000, where there are 20 kinds of amino acids. In nature, each protein
is folded into a well-defined three dimensional structure, the
native structure,
and its functional properties are largely determined by the structure.
(Click the right image to view larger image.)
Protein is a
sequence of amino acids
of length typically less than
1,000, where there are 20 kinds of amino acids. In nature, each protein
is folded into a well-defined three dimensional structure, the
native structure,
and its functional properties are largely determined by the structure.
(Click the right image to view larger image.)
We approximate native protein structures by a
folded sequence of tetrahedrons,
where the shape of the tetrahedron sequence is given as a trajectory of
some discrete differential vector field of tetrahedron tiles. To absorb
irregularity of actual protein structures, we allow rotation
and translation of tetrahedron tiles.
[NOTE] "D2
code"
is an alias of the 5-tile
code.
Recall that
the 5-tile code is the second derivative of the corresponding
tetrahedron sequence.
(2)
Discrete differential geometry of n-simplices
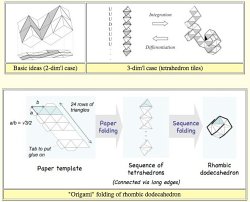 Let's
consider unit cubes and pile
them up in the direction from
(1,1,1) to (-1,-1,-1). And view the resulting surface from above. Then,
if one prints diagonal lines on the upper faces of each cube, he/she
obtains a drawing made up of the diagonal lines, which defines a flow of triangle tiles (2-simplices). If we
consider unit cubes in the four-dimensional space, we would
obtain a flow of
tetrahedron tiles
(3-simplices). Moreover,
any trajectory of tetrahedrons could be implemented by "origami"
folding. (Click the right
image to view larger image.)
Let's
consider unit cubes and pile
them up in the direction from
(1,1,1) to (-1,-1,-1). And view the resulting surface from above. Then,
if one prints diagonal lines on the upper faces of each cube, he/she
obtains a drawing made up of the diagonal lines, which defines a flow of triangle tiles (2-simplices). If we
consider unit cubes in the four-dimensional space, we would
obtain a flow of
tetrahedron tiles
(3-simplices). Moreover,
any trajectory of tetrahedrons could be implemented by "origami"
folding. (Click the right
image to view larger image.)
See the
PROGRAMS section for HeteroNumberViewer
to
view closed tetrahedron trajectories of affine vector fields.
(2.1)
Examples
of Surface Flow
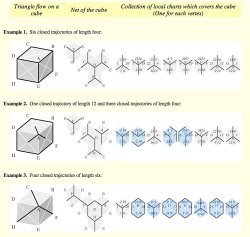 One
could describe
triangle
flows on a cube, using a collection of overlapping local
"flat" charts which cover the cube as shown on the right. Note that
the bottom flow of triangles (example 3) in the figure could
be extended to
a flow of
tetrahedrons,
which is obtained by partitioning a
rhombic dodecahedron into four identical parts as shown in the
figure of section (4) below. (Click the right image to view larger
image.)
One
could describe
triangle
flows on a cube, using a collection of overlapping local
"flat" charts which cover the cube as shown on the right. Note that
the bottom flow of triangles (example 3) in the figure could
be extended to
a flow of
tetrahedrons,
which is obtained by partitioning a
rhombic dodecahedron into four identical parts as shown in the
figure of section (4) below. (Click the right image to view larger
image.)
[NOTE] A trajectory of d-simplices
induces a flow of (d-1)-simplices
on its surfaces.
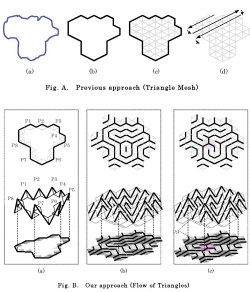 Let’s
consider the two-dimensional object of Fig.A (a), which is
approximated by a polygon of 16 vertices as shown in Fig. A
(b). (Click the right image to view larger
image.)
Let’s
consider the two-dimensional object of Fig.A (a), which is
approximated by a polygon of 16 vertices as shown in Fig. A
(b). (Click the right image to view larger
image.)
(2-2-1) "Triangle mesh"
representation
Fig. A (c) shows a division of the object into 72 triangle
pieces, where we should solve the following two problems: (i) could we
connect all the triangles contained in the object to form a chain which visits
each triangle exactly once and also returns to the
starting triangle (Hamiltonian path)?,
and (ii) how should we decompose
the object to obtain a set of Hamiltonian paths of
triangles which cover the object.
Because it is extremely time-consuming to search a
Hamiltonian path, we often end up
with a
set of short chains as shown in Fig. A (d), where chains are
terminated when they come to the boundary edges.
(2-2-2) "Flow of triangles"
representation
According to the discrete differential geometry of triangles, once the
boundary is given (Fig. B (a)),
connections over all the triangles contained in the object are
uniquely determined. In the case of Fig. A (a), the object is
represented by a flow of triangles with one hole which is consisted of
10
triangles
as shown in Fig. B (b).
Putting one more unit cube (colored red), we obtain another
representation as shown in Fig. B (c). Now, the object is decomposed
into two parts, each of which is represented by a flow of triangles
without any hole.
(3)
Protein complexes
 Recall
that we use weights in scales for weighing objects and a ruler
to measure their length. Biological processes, such as signal
transmission, cell-fate
regulation, transcription, and so on, are not performed by freely
diffusing and occasionally colliding proteins. Instead, proteins
usually do their jobs by forming structured ensemble of proteins, i.e. protein
complexes. The schematic figures on the
right show two notable features of the
formation of protein
complexes. (Click the right image to view larger image.)
Recall
that we use weights in scales for weighing objects and a ruler
to measure their length. Biological processes, such as signal
transmission, cell-fate
regulation, transcription, and so on, are not performed by freely
diffusing and occasionally colliding proteins. Instead, proteins
usually do their jobs by forming structured ensemble of proteins, i.e. protein
complexes. The schematic figures on the
right show two notable features of the
formation of protein
complexes. (Click the right image to view larger image.)
Assigning hetero numbers to proteins and their complexes, we could
describe the formation of protein complexes as additon of the
corresponding
hetero numbers.
(4) Hetero
numbers
 Recall
that we use weights in scales for weighing objects and a ruler
to measure their length. Hetero
numbers
are a system of units for measuring shape of objects such as proteins.
See the
PROGRAMS
section for HeteroNumberViewer
to view
the 3-dim'l hetero numbers.
Recall
that we use weights in scales for weighing objects and a ruler
to measure their length. Hetero
numbers
are a system of units for measuring shape of objects such as proteins.
See the
PROGRAMS
section for HeteroNumberViewer
to view
the 3-dim'l hetero numbers.
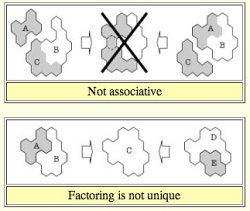
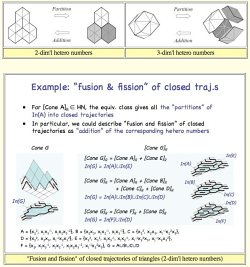
Roughly speaking, d-dim'l
hetero
numbers are a subset of closed affine trajectories
of d-simplex
tiles, where "fusion and fission" of closed trajectories
is described
algebraically. (Click the right image to view
larger image.)
(5) Specification
of hetero numbers
Recall that complex
numbers are defined as a root of a
polynomial equation. We would like to specify hetero
numbers in a similar way:
- Plan A:
Define simultaneous
equations, where a given hetro number is
specified as a root
of equations.
- Plan B:
Design a parallel
programmming language, where
a given hetero number is specified as the semactics
of a program.
(A) Related topics
(A.1)
Programmable Matter
(A.2) Self-reconfigurable
robotics
- External Actuation for Modular Robotics: The
RATChET System (2009, 2010)
- SJET

 Protein is a
sequence of amino acids
of length typically less than
1,000, where there are 20 kinds of amino acids. In nature, each protein
is folded into a well-defined three dimensional structure, the
native structure,
and its functional properties are largely determined by the structure.
(Click the right image to view larger image.)
Protein is a
sequence of amino acids
of length typically less than
1,000, where there are 20 kinds of amino acids. In nature, each protein
is folded into a well-defined three dimensional structure, the
native structure,
and its functional properties are largely determined by the structure.
(Click the right image to view larger image.)




